
A Calibration Management Specialist's Guide to Measurement Uncertainties.
In this article we discuss, in general terms, the principle of measurement uncertainty before turning our attention to a more detailed look at Type-B uncertainties.
1. Introduction
Performing calibrations is an accurate and demanding task. We work with the best instruments at our disposal, ensuring that everything we use is traceably calibrated. We ensure that all our measurements are taken in accordance with appropriate procedures and methods, and that all data is clearly and accurately recorded and presented.
We do not, however, live in a perfect world. We must be honest both to ourselves and to those using the calibration data that we produce. A key element of this honesty is an accurate statement of measurement uncertainty. Some calibration engineers mistakenly view uncertainties as a measure of the accuracy of their work, and the diligence with which it was performed. Nothing could be further from the truth. It its merely an acceptance of the fact that perfection can be strived for but never attained.
Measurement Uncertainties are nothing new. As a young Physics undergraduate, over 40 years ago, no reported measurement would be considered complete unless it was accompanied by a statement of "experimental errors" as they were called in those days. They are now referred to as "measurement uncertainties" for 2 reasons:
|
The word "error" now has another specific use: the numerical difference between the actual value (the measurand) and the observed value of the measurand. This does not include:
* Misreading of instruments such as analogue gauges * Failure to apply known correction factors to raw data * Incorrect recording or misinterpretation of experimental data These are simply mistakes that must be avoided. |
|
| As we mentioned earlier, people do not feel comfortable with the word "error" since it can be misinterpreted as an assesment of the quality of their work. |
2. What are Measurement Uncertainties?
Let's start by definining a few terms:
|
| |
| The Measurand | This is the actual value of the quantity we are attempting measure. |
| The Observed Value | The value that we measure as our interpretation of the measurand. |
| Measurement Error | This is the difference between the Observed Value and the Measurand. |
An overall measurement uncertainty will consist of contributions from a number of components. Some of these components are estimated on the basis of the statistical distribution of a series of measurements and are characterized by experimental standard deviations. These are called Type A evaluation, and will be discussed in detail in other article on this website.
Another type of uncertainty component is known as Type B. Values for Type B evaluation are based on information obtained from either an outside source, or scientific judgment and experience based on all available information. Values belonging in this category may be derived from:
| * | Previous measurement data |
| * | Experience with or general knowledge of the behavior and properties of relevant materials and instruments |
| * | Manufacturer’s specifications |
| * | Data provided in calibration and other certificates |
| * | Uncertainties assigned to reference data taken from handbooks |
The measurement uncertainty for any given calibration is the combination of all the Type A and Type B uncertainty components that occur in the calibration.
The first stage to obtaining an overall (or "combined") uncertainty of a calibration is to list all of the instruments that are used in the calibration. Next you must measure, or, more likely obtain from the manufacturer, all uncertainty values for each instrument, together with either a "coverage factor" or probalbility distribution, both of which are explained later.
You must also include in your list any other factors (ambient temperature, relative humidity, electromagnetic interference, etc) that might influence result of your calibration. The completed list is called an "Uncertainty Budget".
3. Type-B Measurement Uncertainties.
In practice you will find that there are only 2 kinds of Type B uncertainty in common use:
|
|
Uncertainty value obtained from an outside source |
|
|
Uncertainty value obtained from an assumed probability distribution |
Since contributions obtained from an outside source are pretty straight-forward, let us now look at values obtained from an assumed probability distribution in more detail:
Have a look at the picture below. The graphs represent the results of a large number of repeat measurements of a value. The horizontal axis represents the measured value and the vertical axis represents the number of measurements with that value.
In all 3 diagrams we are making a series of repeat measurements of a parameter whose actual value is M (the measurand). We know that the tolerance on our measurement is ±a. So all measurements (correctly made) will lie between the vales of M+a and M-a. Now, if it is just as likely for a measurement to be any value between these limits, we would say that its probabiity distribtion is "rectangular" (sometimes also known as "uniform") as in the centre picture.
A triangular or normal distribution would be used when the values of the quantity are known to be more likely near the center of the limits. These are shown in the left and right-hand pictures.
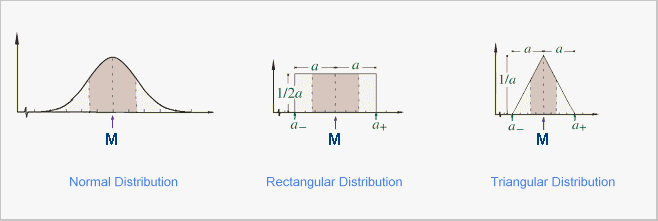
In all 3 cases, we should expect that the mean of all our measurements will be the value M, that of our measurand. If it is not, there is some systematic error that needs to be eliminated or compensated for.
4. Expression of Uncertainties.
There is no prescribed method for reporting uncertainties. Statements just need to be clear and concise. Here are a few good examples:
|
|
The mass of the weight under test was measured as 10,000.005 g with an associated expanded uncertainty of 45 mg (coverage factor k=2), Type B rectangular distribution. |
|
|
The reported uncertainty is based on a standard uncertainty multiplied by a coverage factor k = 2, which provides a confidence level of approximately 95 %. The standard uncertainty has been determined in accordance with EA 04/2. |
|
|
The combined standard uncertainty includes the standard uncertainty reported for the standard, the standard uncertainty for the measurement process, the standard uncertainty for any uncorrected errors associated with buoyancy corrections, and a component of uncertainty to account for any observed deviations from NIST values that are less than surveillance limits.
The combined standard uncertainty is multiplied by a coverage factor of 2 to give an expanded uncertainty, which defines an interval having a level of confidence of approximately 95 percent. The expanded uncertainty presented in this report is consistent with the 1993 ISO Guide to the Expression of Uncertainty in Measurement. The expanded uncertainty is not to be confused with a tolerance limit for the user during application. |
5. Best Measurement Capability.
Best measurement capability (always referring to a particular quantity, the measurand) is defined as the smallest uncertainty of measurement that a laboratory can achieve within its scope of accreditation, when performing more or less routine calibrations of nearly ideal measurement standards or measuring instruments designed for the measurement of that quantity. The assessment of best measurement capability of accredited calibration laboratories is based on the method described in the accreditation document, and will normally be supported or confirmed by experimental evidence.
Again it is a fact of life that reducing measurement uncertainties costs money, but a well performed uncertainty budget will indicate where uncertainties can be reduced at least cost.
5. Useful Links
Here are some links that you might find informative:
